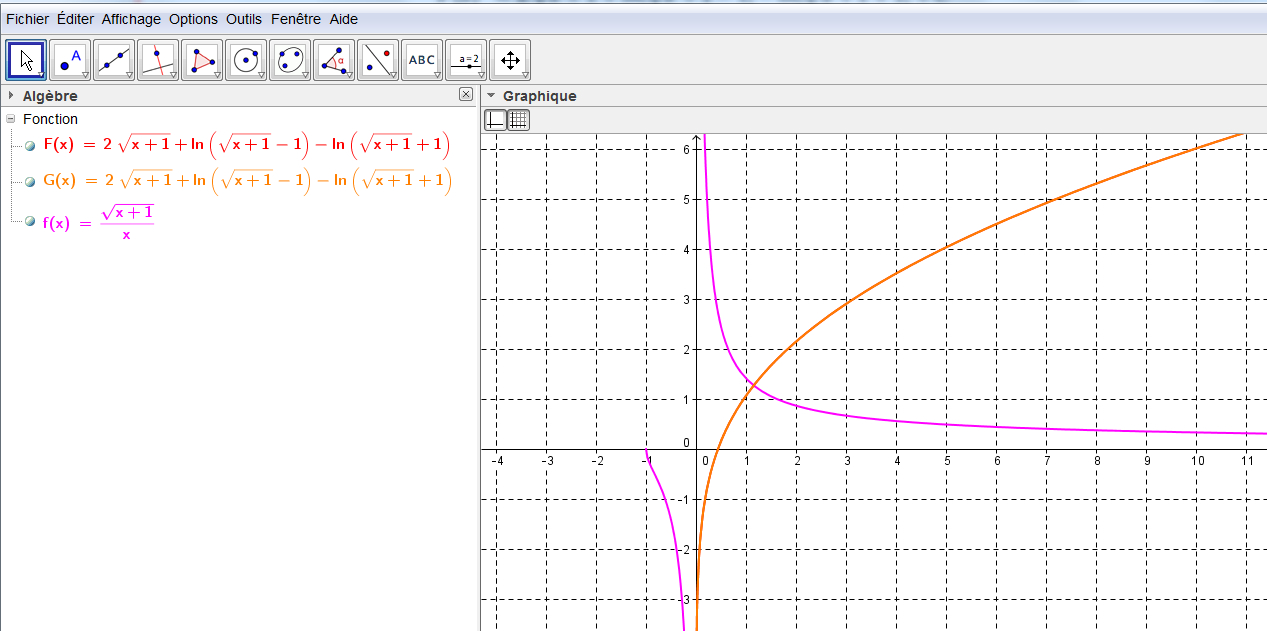
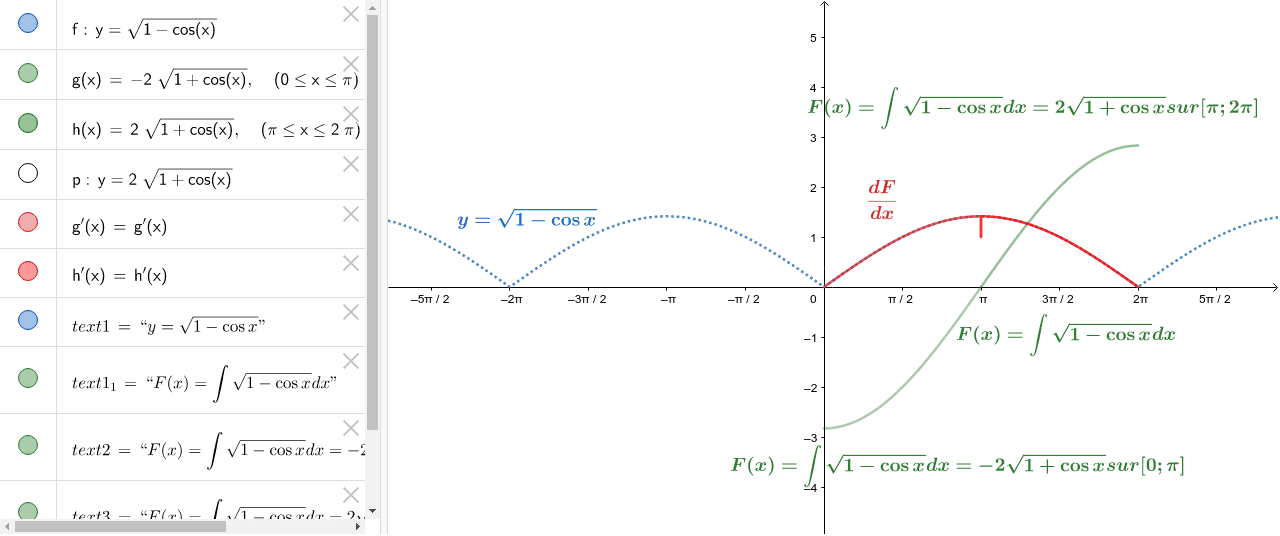
Dl De Racine De 1 X

La question est donc de trouver le DL de 1/g(x) à partir de celui de g(x). Pour ce faire, nous allons utiliser le DL de 1/(1+x) ou 1/(1-x) selon les cas, et effectuer un changement de variable. Commençons par un cas simple, celui de 1/cos(x) (qui servira à calculer le DL.
(Définition) En mathématiques, un développement limité d'une fonction au voisinage d'un point considéré est une expression polynomiale permettant une approximation de de.
Développements limités usuels Les développements limités ci-dessous sont valables quand x tend vers 0 et uniquement dans ce cas. Formule de Taylor-Young en 0. f(x) =
Calculateur de radicaux et racines en ligne. Calculez la racine n-ième de x. Entrez le degré racine (n) et le nombre (x) et appuyez sur le bouton =.
Tu veux développer. racine (x) au voisinage de 2, et tu le connais au voisinage de 1... Tu peux donc écrire x=2* (x/2) avec x/2 qui tend vers 1. Ainsi, racine (x)=racine.
Re : Développement limité racine carrée. En admettant que je laisse la racine telle quelle et que je travaille dessus après, je peux bidouiller qqch. Mais je suis alors.
Je n'arrive pas à prouver ceci : soit P la partie principale du DL de racine de 1+x à l'ordre n Mq P²-X-1 est divisible par X^(n+1) J'ai essayé pas mal de choses et rien ne va.
Le principe est le suivant : s'il existe une solution à l'équation f (x) = 0 f(x)=0 sur l'intervalle [a, b] [a,b], c'est que, avec m = a + b 2 m=\frac{a+b}{2}, l'une (au moins) des deux.
La dérivée k -ième de f ( x) = ( 1 + x) α s’écrit : f ( k) ( x) = α ( α − 1) ⋯ ( α − k + 1) ( 1 + x) α − k. En x = 0, f ( k) ( 0) = α ( α − 1) ⋯ ( α − k + 1) f est de classe C n sur un.
comment on obtient "-1/32 x" dans -1/8( 1/16x² -1/32 x) a la deuxieme ligne, dl de racine](1+racine (1+x)) ordre 3 en 0 = racine de (2) * (1 + 1/4x + 1/16x²+ 1/32 x^3 +.
Messages 2 Développement limité d'une racine et limite ------ Bonjour à tous , Je viens vous demander un peu d'aide pour un exercice qui me pose problème ,j'ai.
D.L de racine (1+cos (x)) Écrire une nouvelle question 11 messages - Page 1 sur 1 Siouar88 Messages: 7 Enregistré le: Mar 30 Déc 2008 23:23 par Siouar88 » Mer.
Effectivement, la DL de sqrt (1+x) s'obtient à partir du DL de (1+x)âlpha, avec alpha = 1/2 car tout nombre élevé à la puissance 1/2 donne sa racine. carrée. Cela vient du.
je cherche le developpement limité d'ordre 2 en 0 de rac(1+x 2) donc je procede de cette facon : (1+x 2 )^1/2 = 1+(x 2 /2)+(-x 4 /8) o(x 2 ) = 1+(x 2 /2)+(x 4.
salut, en fait j'avais une liste de developpements limités à faire j'en ait fait la plupart mais je n'arrive pas à cela, celui avec la racine je vois pas du tout mais en fait je.
bonjour à tous et à toutes j'ai un controle d'analyse lundi et j'aimerais savoir comment calculer le DL2 (0) de la fonction suivante : f (x)=1/ ( 1+x) je sais que c'est un.
DL de racine de 1+X. Posté par usul 31-10-11 à 02:43. bonjour. dans le resultat suivant je ne comprend pas, comment on obtient "-1/32 x" dans -1/8 ( 1/16x² -1/32 x) a la.
Bonjour, Je voudrais savoir comment faire le devellopement limité de racine de ch x à l'ordre 4 en x=0 ? toggle menu Les-mathematiques.net Les-mathematiques.net.
DL de racine Cos (x) 1 sur 1. Gringo40. Messages : 4. Enregistré le : 31 déc. 2011 22:03.
DL de la racine carrée. La racine carrée a le développement limité. Explication. Nous ne pouvons pas travailler avec , parce que la première dérivée pour la racine carrée,.
Dl De Racine De 1 X - Communauté MCMS












Vous pourriez aussi aimer
- 100 Sleeping Princes The Kingdom Of Dreams Characters
- Duree De Vie D Un Perroquet
- Bully In Charge 57
- Sujet Brevet 2022 Français Corrigé
- Comment Restaurer La Page D Accueil Orange
- Coloriage Bonnes Vacances Maternelle
- Harry Potter Dessin Facile
- Quelle Est La Marque De Voiture De Flash Mcqueen
- Cancer De La Peau Photo Visage
- Villain To Kill Scan 107
- Dessin Harry Potter Facile A Reproduire
- Page De Garde Physique Chimie 6ème
- L ile Au Trésor Resume Par Chapitre
- Undead Unluck Tome 2 Date De Sortie France
- Correction Sujet Brevet Histoire 2023
- One Piece 1088 Read
- Site Pour Regarder Des Series Turques En Francais
- Blue Moon
- Page De Garde Poésie Cp
- Tensei Shitara Slime Datta Ken Saison 2 Vostfr
